22.1.1二次函数 同步测试
待定系数法求二次函数的分析式
1、选择题
1. 已知一条抛物线经过E(0,10),F(2,2),G(4,2),H(3,1)四点,选择其中两点用待定系数法能求出抛物线分析式的为()
A.E,F B.E,G C.E,H D.F,G
2.二次函数![]() 有
有
A.最小值-5 B.最大值-5 C.最小值-6 D.最大值-6
3.把抛物线y=3x2先向上平移2个单位再向右平移3个单位,所得的抛物线是( )
A. y=32+2 B.y=32+2 C.y=32-2 D. y=32-2
4.如图所示,已知抛物线y=![]() 的对称轴为x=2,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为,则点B的坐标为
的对称轴为x=2,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为,则点B的坐标为
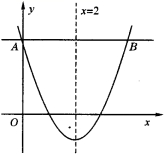
A. B. C. D.
5.将函数![]() 的图象向右平移a个单位,得到函数
的图象向右平移a个单位,得到函数![]() 的图象,则a的值为
的图象,则a的值为
A.1 B.2 C.3 D.4
6.若二次函数![]() 的x与y的部分对应值如下表:
的x与y的部分对应值如下表:
x | -7 | -6 | -5 | -4 | -3 | -2 |
Y | -27 | -13 | -3 | 3 | 5 | 3 |
则当x=1时,y的值为
A.5 B.-3 C.-13 D.-27
2、填空题
7.抛物线![]() 的图象如图所示,则此抛物线的分析式为__________________.
的图象如图所示,则此抛物线的分析式为__________________.


第7题 第10题
8.已知A(0,3),B(2,3)是抛物线y=﹣x2+bx+c上两点,该抛物线的顶点坐标是______________________________.
9.已知抛物线![]() .该抛物线的对称轴是________,顶点坐标________;
.该抛物线的对称轴是________,顶点坐标________;
10.如图所示已知二次函数![]() 的图象经过点(-1,0),(1,-2),当y随x的增大而增大时,x的取值范围是__________________.
的图象经过点(-1,0),(1,-2),当y随x的增大而增大时,x的取值范围是__________________.
11.已知二次函数![]() 中自变量x和函数值y的部分对应值如下表:
中自变量x和函数值y的部分对应值如下表:
| … |
| -1 |
| 0 |
| 1 |
| … |
| … |
| -2 |
| -2 |
| 0 |
| … |
则该二次函数的分析式为__________________.
12.已知抛物线![]() 的顶点坐标为,且与x轴两交点间的距离为4,则抛物线的分析式为__________________.
的顶点坐标为,且与x轴两交点间的距离为4,则抛物线的分析式为__________________.
3、解答卷
13.依据下列条件,分别求出对应的二次函数分析式.
已知抛物线的顶点是,且过点;
已知二次函数的图象经过,,三点;
已知抛物线与x轴交于点,,且图象过点.
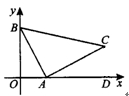
14.如图,已知直线y=-2x+2分别与x轴、y轴交于点A,B,以线段AB为直角边在第一象限内作等腰直角三角形ABC,∠BAC=90°,求过A、B、C三点的抛物线的分析式.
15.如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A、C分别在x轴、y轴的正半轴,抛物线y=﹣![]() x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC、BD、CD.
x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC、BD、CD.
(1)求此抛物线的分析式.
(2)求此抛物线顶点D的坐标和四边形ABCD的面积.
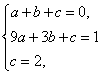
答案与分析
1、选择题
1.【答案】C.
【分析】∵F(2,2),G(4,2),
∴F和G点为抛物线上的对称点,
∴抛物线的对称轴为直线x=3,
∴H(3,1)点为抛物线的顶点,
设抛物线的分析式为y=a(x﹣3)2+1,
把E(0,10)代入得9a+1=10,解得a=1,
∴抛物线的分析式为y=(x﹣3)2+1.
2.【答案】C;
【分析】第一将一般式通过配方化成顶点式,即![]()
![]() ,
,
∵ a=1>0,∴ x=-1时,![]() .
.
3.【答案】A;
4.【答案】D;
【分析】∵ 点A,B均在抛物线上,且AB与x轴平行,
∴ 点A与点B关于对称轴x=2对称,
又∵ A,
∴ AB=4,yB=yA=3,
∴ 点B的坐标为.
5.【答案】B;
【分析】抛物线的平移可看成顶点坐标的平移,![]() 的顶点坐标是
的顶点坐标是![]() ,
,![]() 的顶点坐标是
的顶点坐标是![]() ,∴ 移动的距离
,∴ 移动的距离![]() .
.
6.【答案】D;
【分析】此题假如先用待定系数法求出二次函数分析式,再将x=1代入求函数值,显然太繁,
而由二次函数的对称性可飞速地解决此问题.
察看表格中的函数值,可发现,当x=-4和x=-2时,函数值均为3,由此可知对称轴
为x=-3,再由对称性可知x=1的函数值必和x=-7的函数值相等,而x=-7时y=-27.
∴ x=1时,y=-27.
2、填空题
7.【答案】![]() ;
;
【分析】由图象知抛物线与x轴两交点为,,则![]() .
.
8.【答案】(1,4).
【分析】∵A(0,3),B(2,3)是抛物线y=﹣x2+bx+c上两点,
∴代入得:![]() ,
,
解得:b=2,c=3,
∴y=﹣x2+2x+3
=﹣(x﹣1)2+4,
顶点坐标为(1,4),
故答案为:(1,4).
9.【答案】x=1;;
【分析】代入对称轴公式![]() 和顶点公式
和顶点公式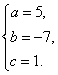 即可.
即可.
10.【答案】![]() ;
;
【分析】将,代入![]() 中得b=-1,
中得b=-1,
∴ 对称轴为![]() ,在对称轴的右边,即
,在对称轴的右边,即![]() 时,y随x的增大而增大.
时,y随x的增大而增大.
11.【答案】![]() ;
;
【分析】此题以表格的形式给出x、y的一些对应值.要认真剖析表格中的每一对x、y值,
从中选出较简单的三对x、y的值即为,,,再设一般式![]() ,
,
用待定系数法求解.
设二次函数分析式为![]() ,
,
由表知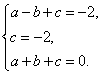 解得
解得
∴ 二次函数分析式为![]() .
.
12.【答案】![]() ;
;
【分析】由题意知抛物线过点和.
3、解答卷
13.【答案与分析】
∵ 顶点是,
∴ 设![]() .
.
又∵ 过点,∴ ![]() ,∴ a=1.
,∴ a=1.
∴ ![]() ,即
,即![]() .
.
设二次函数分析式为![]() .
.
由函数图象过三点,,得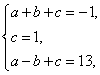 解得
解得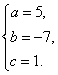
故所求的函数分析式为![]() .
.
由抛物线与x轴交于点,,
∴ 设y=a,又∵ 过点,
∴ a=-3,∴ a=-1,
∴ y=-,即![]() .
.
14.【答案与分析】
过C点作CD⊥x轴于D.
在y=-2x+2中,分别令y=0,x=0,得点A的坐标为,点B的坐标为.
由AB=AC,∠BAC=90°,得△BAO≌△ACD,
∴ AD=OB=2,CD=AO=1,
∴ C点的坐标为.
设所求抛物线的分析式为![]() ,
,
则有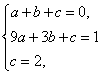 ,解得
,解得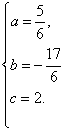 ,
,
∴ 所求抛物线的分析式为![]() .
.
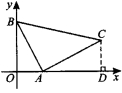
15.【答案与分析】
解:(1)由已知得:C(0,4),B(4,4),
把B与C坐标代入y=﹣![]() x2+bx+c得:
x2+bx+c得:![]() ,
,
解得:b=2,c=4,
则分析式为y=﹣![]() x2+2x+4;
x2+2x+4;
(2)∵y=﹣![]() x2+2x+4=﹣
x2+2x+4=﹣![]() (x﹣2)2+6,
(x﹣2)2+6,
∴抛物线顶点坐标为(2,6),
则S四边形ABDC=S△ABC+S△BCD=![]() ×4×4+
×4×4+![]() ×4×2=8+4=12.
×4×2=8+4=12.







