延安中学2018-2019学年度高中三年级9月份开学摸底考试数学试题
1、填空题
1.已知全集
则集合
________.
2.若
,则
________.
3.1、1、3、3、5这五个数的中位数是________.
4.假如函数
的反函数为
,那样
的值为_______.
5.若数列的前
项和
,则通项
________.
6.三阶行列式
中,元素-3的代数余子式的值为_______.
7.过定点p,且倾斜角是直线
的倾斜角两倍的直线方程为________.
8.若无穷等比数列的各项和
的值为2,则首项
的取值范围为________.
9.已知关于
的方程的两根为
,满足
,则实数
的值为__.
10.已知O是坐标原点,点A,若点M
为平面区城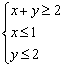
内的一个动点，则
的取值范围是__________.
11.设集合
则集合A中满足条件：
“”的元素个数为__________.
12.设
函数
若函数
与的图象有且仅有两个不一样的公共点,则的取值范围是____________.
2、选择题
13.已知是实数,那样“
”是“
”的
A.充分而非必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也非必要条件
14.若两个球的体积之比为8:27,则它们的表面积之比为
A.2:3 B.4:9 C.8:27 D.
15.设单位向量
和
既不平行也不垂直,对非零向量，有结论:①若
则
；②若，则,关于以上两个结论,正确的判断是
A.①成立,②成立 B.①不成立,②不成立
C.①成立,②不成立 D.①不成立,②成立
16.由9个正数组成的矩阵
中,每行中三个数成等差数列，且
成等比数列,给出下列判断:①第2列中的必成等比数列；②第1列中的未必成等比数列；③
；④若9个数之和等于9,则,其中正确的个数为
A.1 B.2 C.3 D.4
3、解答卷
17.
如图,在长方体
中,AB=BC=2,
求四棱锥
的体积；
求异面直线与所成角的大小.
18.
在△ABC中,角A、B、C所对的边长分别为.
若
且△ABC的面积,求
的值；
若,试判断△ABC的形状.
19.
已知美国苹果公司生产某款 iPhone手机的年固定本钱为40万USD,每生产1万部还需要另
外投入16USD,设苹果公司一年内共生产该款 iPhone手机
万部并全部销售完,每万部的
销售收入为
万USD,且.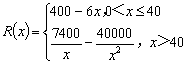
写出年收益
关于年产量的函数分析式；
当年产量为多少万部时，苹果公司在该款手机的生产中所获得的价值最大?并求出最大收益。
20.
已知双曲线
经过点,两条渐近线的夹角为
直线交双曲线于A、B.
求双曲线C的方程；
若过原点,P为双曲线上异于A、B的一点,且直线PA、PB的斜率均存在。
求证：
为定值；
若过双曲线的右焦点,是不是存在轴上的点M,使得直线绕点无论如何转动,都有成立?若存在,求出M的坐标；若没有,请说明理由。
21.
已知是公差为的等差数列,
是公比为的等比数列。
若
是不是存在有?请说明理由；
若
对任意有,试求出满足的充要条件；
若
,试确定所有,使数列中存在某个连续项的和是数列中的一项,请证明。
